계층 군집(Hierarchical clustering)
프로토타입 기반 군집의 또 다른 방법이다.
계층 군집은 덴드로그램(dendrogram)을 그릴 수 있어 의미 있는 분류 체계를 시각적으로 이해하기 쉽다.
또한 클러스터 개수를 미리 지정할 필요가 없다.
계층 군집에는 병합계층 군집(agglomerative hierarchical clustering)과 분할 계층 군집(divisive hierarchical clustering)이 있다.
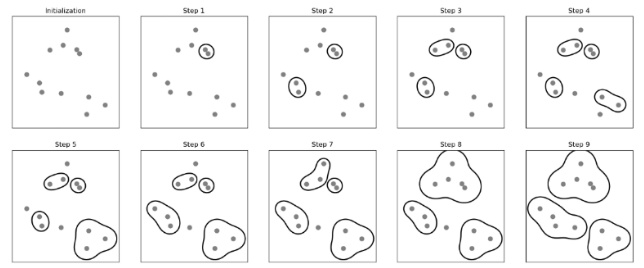
병합 계층 군집
분할 계층 군집(divisive hierarchical clustering)
분할 군집에서는 전체 샘플을 포함하는 하나의 클러스터에서 시작하여 더 작은 클러스터로 반복적으로 나눈다.
이는 클러스터 안에 샘플이 하나만 남을 때까지 계속된다.
병합 계층 군집(agglomerative hierarchical clustering)
분할 계층 군집과 달리 각 샘플이 독립적인 클러스터가 되고 하나의 클러스터가 남을 때까지 가장 가까운 클러스터를 합친다.
병합군집
상향식으로 클러스터 묶기
병합 계층 군집의 두 가지 기본 알고리즘은 단일 연결(single linkage)과 완전 연결(complete linkage)이다.
단일 연결은 클러스터 쌍에서 가장 비슷한 샘플 간 거리를 계산한다.
그 다음 가장 거리가 작은 두 클러스터를 합친다.
완전 연결 방식은 클러스터 쌍에서 가장 비슷하지 않은 샘플을 비교하여 병합을 수행한다.
평균 연결(average linkage)는 두 클러스터에 있는 모든 샘플 사이의 평균 거리가 가장 작은 클러스터 쌍을 합친다.
와드 연결은 클러스터 내 SSE가 가장 작게 증가하는 두 클러스터를 합친다.
Process of agglomerative hierarchical clustering(complete linkage)
1. 모든 샘플의 거리 행렬을 계산한다.
2. 모든 데이터 포인트를 단일 클러스터로 표현한다.
3. 가장 비슷하지 않은(멀리 떨어진)샘플 사이 거리에 기초하여 가장 가까운 두 클러스터를 합친다.
4. 유사도 행렬을 업데이트한다.
5. 하나의 클러스터가 남을 때까지 2-4단계를 반복한다.
import pandas as pd
import numpy as np
np.random.seed(123)
variables=['X', 'Y', 'Z']
labels=['ID_0', 'ID_1', 'ID_2', 'ID_3', 'ID_4']
X=np.random.random_sample([5, 3])*10
df=pd.DataFrame(X, columns=variables, index=labels)
df
X Y Z
ID_0 6.964692 2.861393 2.268515
ID_1 5.513148 7.194690 4.231065
ID_2 9.807642 6.848297 4.809319
ID_3 3.921175 3.431780 7.290497
ID_4 4.385722 0.596779 3.980443
거리 행렬
scipy.spatial.distance의 pdist를 사용해서 거리 행렬을 계산한다.
from scipy.spatial.distance import pdist, squareform
row_dist=pd.DataFrame(squareform(pdist(df, metric='euclidean')), columns=labels, index=labels)
row_dist
ID_0 ID_1 ID_2 ID_3 ID_4
ID_0 0.000000 4.973534 5.516653 5.899885 3.835396
ID_1 4.973534 0.000000 4.347073 5.104311 6.698233
ID_2 5.516653 4.347073 0.000000 7.244262 8.316594
ID_3 5.899885 5.104311 7.244262 0.000000 4.382864
ID_4 3.835396 6.698233 8.316594 4.382864 0.000000
완전 연결 병합 적용, 연결 행렬 반환
scipy.cluster.hierarchy 모듈의 linkage함수를 이용해서 완전 연결 병합을 적용한 후 연결 행렬을 반환 받는다.
from scipy.cluster.hierarchy import linkage
help(linkage)
Help on function linkage in module scipy.cluster.hierarchy:
linkage(y, method='single', metric='euclidean', optimal_ordering=False)
Perform hierarchical/agglomerative clustering.
The input y may be either a 1-D condensed distance matrix
or a 2-D array of observation vectors.
If y is a 1-D condensed distance matrix,
then y must be a :math:`\binom{n}{2}` sized
vector, where n is the number of original observations paired
in the distance matrix. The behavior of this function is very
similar to the MATLAB linkage function.
A :math:`(n-1)` by 4 matrix ``Z`` is returned. At the
:math:`i`-th iteration, clusters with indices ``Z[i, 0]`` and
``Z[i, 1]`` are combined to form cluster :math:`n + i`. A
cluster with an index less than :math:`n` corresponds to one of
the :math:`n` original observations. The distance between
clusters ``Z[i, 0]`` and ``Z[i, 1]`` is given by ``Z[i, 2]``. The
fourth value ``Z[i, 3]`` represents the number of original
observations in the newly formed cluster.
linkage 함수는 pdist 함수에서 계산된 축약된 거리 행렬(상삼각 행렬(upper triangular matrix)를 입력으로 사용할 수 있다.
혹은 linkage 함수에 초기 데이터 배열을 전달하고, ‘euclidean’ 지표를 매개변수로 사용할 수 있다.
squareform 함수로 만든 거리 행렬(row_dist)은 사용할 수 없다.(상삼각 행렬이 아님)
축약된 거리행렬을 사용하거나, 원본 샘플 행렬(설계행렬(design matrix))를 사용해서 올바른 연결 행렬을 얻어야 한다.
from scipy.cluster.hierarchy import linkage
row_clusters=linkage(row_dist, method='complete', metric='euclidean')
row_clusters=linkage(pdist(df, metric='euclidean'), method='complete')
row_clusters=linkage(df.values, method='complete', metric='euclidean')
pdist는 원래 상삼각 행렬의 값을 출력
>>> pdist(df, metric='euclidean')
array([4.973534 , 5.51665266, 5.89988504, 3.83539555, 4.34707339,
5.10431109, 6.69823298, 7.24426159, 8.31659367, 4.382864 ])
연결 행렬을 DataFrame으로 변환
pd.DataFrame(row_clusters, columns=['row label 1', 'row label 2', 'distance', 'no. of items in clust.'], index=['cluster %d' %(i+1) for i in range(row_clusters.shape[0])])
row label 1 row label 2 distance no. of items in clust.
cluster 1 0.0 4.0 3.835396 2.0
cluster 2 1.0 2.0 4.347073 2.0
cluster 3 3.0 5.0 5.899885 3.0
cluster 4 6.0 7.0 8.316594 5.0
연결 행렬의 행은 클러스터 병합을 나타낸다.
첫 번째와 두 번째 열은 각 클러스터에서 완전 연결 방식으로 병합된 클러스터를 나타낸다.
세 번째 열은 클러스터 간 거리
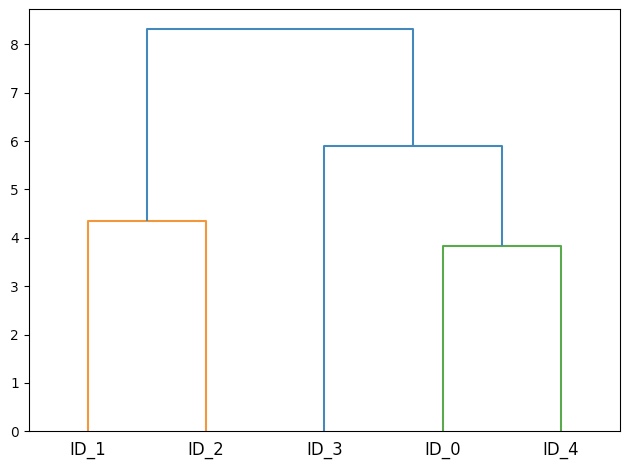
덴드로그램
from scipy.cluster.hierarchy import dendrogram
row_dendr=dendrogram(row_clusters, labels=labels)
plt.tight_layout()
plt.ylabel('Euclidean distance')
plt.show()
Heat map
코드에 대한 설명 참조
머신러닝교과서with파이썬,사이킷런,텐서플로_개정3판pg.463-
fig=plt.figure(figsize=(8, 8), facecolor='white')
axd=fig.add_axes([0.09, 0.1, 0.2, 0.6])
row_dendr=dendrogram(row_clusters, orientation='left')
df_rowclust=df.iloc[row_dendr['leaves'][::-1]]
axm=fig.add_axes([0.23, 0.1, 0.6, 0.6])
cax=axm.matshow(df_rowclust, interpolation='nearest', cmap='hot_r')
axd.set_xticks([])
axd.set_yticks([])
for i in axd.spines.values():
i.set_visible(False)
fig.colorbar(cax)
axm.set_xticklabels(['']+list(df_rowclust.columns))
axm.set_yticklabels(['']+list(df_rowclust.index))
plt.show()
scikit-learn AgglomerativeClustering
사이킷런 병합 군집은 계층 군집의 트리 성장을 일찍 멈추게 할 수 있다.
n_clusters 매개변수를 지정함으로서 군집의 개수를 지정할 수 있다.(꼭 입력하지 않아도 된다.)
from sklearn.cluster import AgglomerativeClustering
ac=AgglomerativeClustering(n_clusters=3, affinity='euclidean', linkage='complete')
labels=ac.fit_predict(X)
print('클러스터 레이블: %s' %labels)
from sklearn.cluster import AgglomerativeClustering
ac=AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='complete')
labels=ac.fit_predict(X)
print('클러스터 레이블: %s' %labels)

![Python 머신러닝] 8장. 군집분석 (Cluster Analysis)](resources/098D576A63A546FE960391DDA8D02819.png)